私立中学では、入試のピークを迎えています。
中２で三平方の定理
さて、そんな中学受験を経験して中高一貫校の2年生になった生徒さんですが、個人指導シグマに在籍している生徒さんは、
数学は”三平方の定理”を学習しております。
一番早い学校は、関西の西大和です。
関西の中高一貫は、相対的に進みが早いです。
都内の中高一貫校は、三平方の定理を学習するのは中2の３学期が多いです。
中には、白百合の様に中3の1・２学期などと言うケースも有ります。
公立の中学では、三平方の定理は中学3年生で学習する単元です。
相似
円
と学習してきて、最後の中学生の範囲となります。
三平方の定理は難しい
三平方の定理の単元は、難しいです。
何故かと言うと、今までに学習したいろいろな分野が混ざっているからです。
2次方程式の計算もちゃんと出来ないと話になりません。
因数分解が出来ないと2次方程式が解けないのは当然です。
円との融合問題
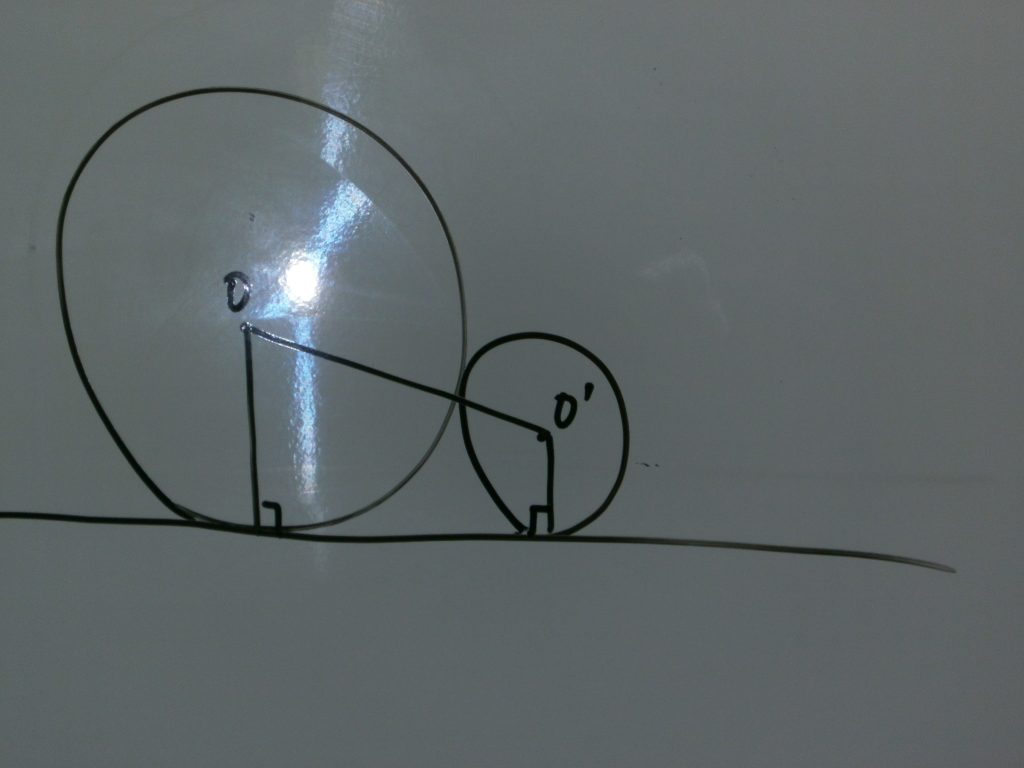
三平方では、円と直線や図形が絡んだ問題があります。
上の問題のようなタイプでは、補助線が必要です。
定期試験によく出る問題ですが、出来ない生徒さんをよく見かけます。
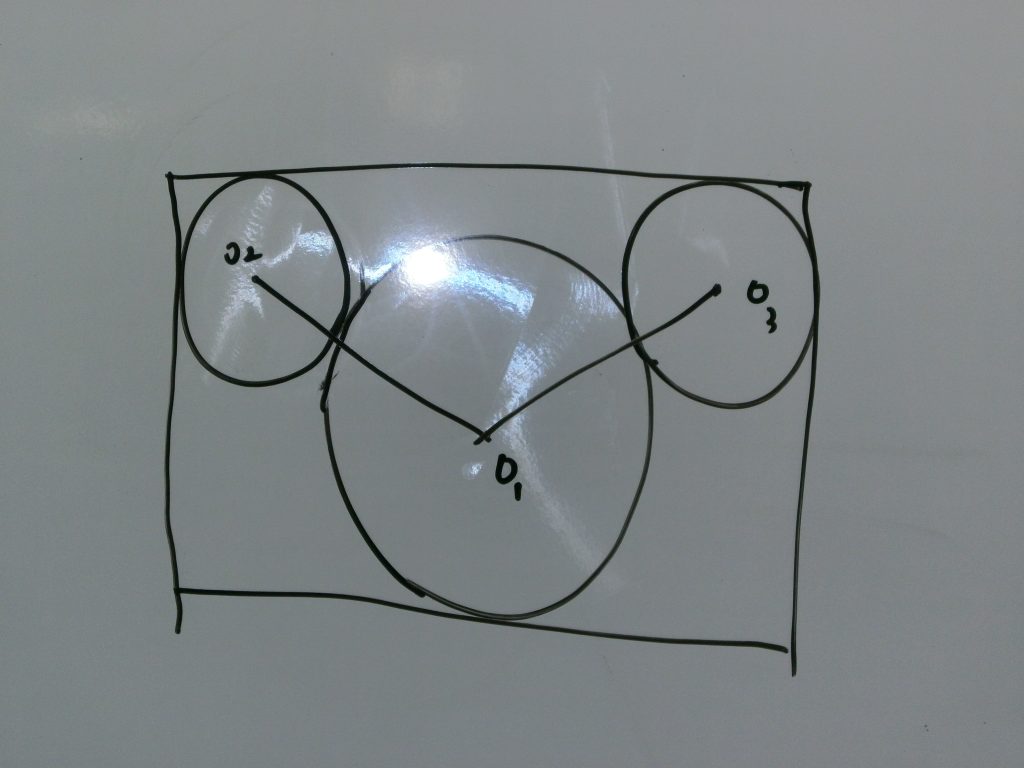
さらに、上のような問題だと補助線の数が増えます。
ここまでくると、お手上げ状態の生徒さんも出てきますね。
でも、安心してください。
ちゃんと、体系数学問題集を解いていれば大丈夫です。
最初は、解けないかもしれません。
解けなかったら、解答をよく見て解き直してください。
そのうち解けるようになります。
相似との融合問題
三平方の定理と相似を絡めた問題もよく見かけます。
”三平方の定理”の単元だからと言ってそれだけで解ける問題ばかりではありません。
線分の長さを求める問題では、相似は大活躍です。
相似が苦手な人も多いですが、試験までに復習しておいた方が良いかもしれませんね。
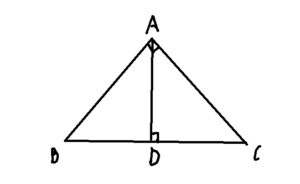
上のような直角三角形ABCにおいて、AからBCに垂線を引いた場合に相似の三角形がいろいろ出てきます。
まず、三角形ABCと三角形DBCは相似です。
同様にして、右の三角形ACDも大きい三角形と左の三角形も全部相似になっています。
直角三角形の問題であれば、三平方の定理はもちろん使えます。
けれども、それだけだTお解けない問題が多いです。
問題のどこかの部分で相似を使って長さを出すのが必要になります。
間違いやすいのは、どこの辺とどこの辺が対応しているのかです。
意外と分かりにくいことが結構あります。
そういう時には、等しい角に注目してその角の対辺という見方をすると対応する辺を間違えることが少なくなります。
空間図形となると
平面だけでも大変な三平方の定理
なんと、立体の問題も出てきます。
切断面を考えないといけない問題は、得手不得手がはっきりと分かれます。
体積を求める問題だと、工夫しないと膨大な計算量となります。
まあ、いきなり空間の問題は解けないので平面の問題が解けるようになってからの方が良いでしょう。
三平方の定理の空間の問題を与えられた図だけを使って、解こうとする人が多いんですが、そのやり方だと解けないことが多いです。
ちゃんとこうとしたら、切断面の平面図をちゃんと書かなければいけません。
切断面の平面図と各頂点をちゃんと記号で記入します。
そういった平面図を何枚か用意して、もともとの見取り図と照らし合わせながら考えるわけです。
空間の問題はその直感的に解くということができる人はそんなに多くありません。
やはり平面図で自分の目で確認して解くっていう作業がどうしても必要になります。
学校の定期テストのレベルで点数を取ろうとしたら、やはりこういった平面図を自分で書かないと始まらないですね。
三平方の定理の範囲の定期試験で点数を取るには
点数が欲しいならば問題演習をやらないといけません。
特に学校から渡されている教材は必ず解きましょう。
一度やっただけで出来ると思っている生徒さんが多いですが、ダメですね。
解けなかった問題は、解き直しをして確実に解けるようになっているか確認することが必要です。
問題によっては、知っていればすぐに解けることもありますよ。
三平方の定理が終わったらいよいよ高校生の範囲に
体系数学で”三平方の定理”が終わるといよいよ高校生の教材に移行します。
そのまま体系数学３を使う学校もありますが、そうでない学校の方が多いようです。
数学に不安を感じている生徒さんは、これまでの範囲の復習をやっておいた方が良いかもしれませんね。
特に、代数の範囲で出来ないところがあると大変なことになります。
体系数学2の次は、普通の高校用の教科書を使うところが多いです。
問題集は、4STEPが多いです。
（一部、サクシードを使っている所が有ります。）
高校の範囲になると差が一気に広がります。
勉強しない人は、一気に置いて行かれます。
そうならないように普段の勉強を頑張らないといけませんね。
学校で参考書をもらうところとそうでない学校があります。
自分で数学の参考書を買うのであれば、フォーカスゴールド”をお勧めします。
今までの、標準であった青チャートよりもカバーできる範囲が広くなっています。
フォーカスゴールドには、大まかな偏差値対応が載っています。
それを見ながら自分が到達しなければいけないレベルを確認しながら勉強を進めると良いでしょう。
個人指導シグマは、中高一貫校専門
オンラインの授業にも対応しています。
体系数学でお困りの方は、お気軽にお問合せください。
大学受験もセンター試験が終わり私立の一般受験本番となっています。
受験を経験し中学生になった生徒さんたちは、学校ごとに進度が違います。
教科書は、ほとんどの学校で体系数学が使われています。（体系数学のまとめはこちら）
公立の中学では、中学3年生で学習する単元です。
中２で三平方の定理
さて、そんな中学受験を経験して中高一貫校の2年生になった生徒さんですが、個人指導シグマに在籍している生徒さんは、
数学は”三平方の定理”を学習しております。
一番早い学校は、関西の西大和です。
関西の中高一貫は、相対的に進みが早いです。
都内の中高一貫校は、三平方の定理を学習するのは中2の３学期が多いです。
中には、白百合の様に中3の1・２学期などと言うケースも有ります。
公立の中学では、三平方の定理は中学3年生で学習する単元です。
相似
円
と学習してきて、最後の中学生の範囲となります。
三平方の定理は難しい
三平方の定理の単元は、難しいです。
何故かと言うと、今までに学習したいろいろな分野が混ざっているからです。
2次方程式の計算もちゃんと出来ないと話になりません。
因数分解が出来ないと2次方程式が解けないのは当然です。
円との融合問題
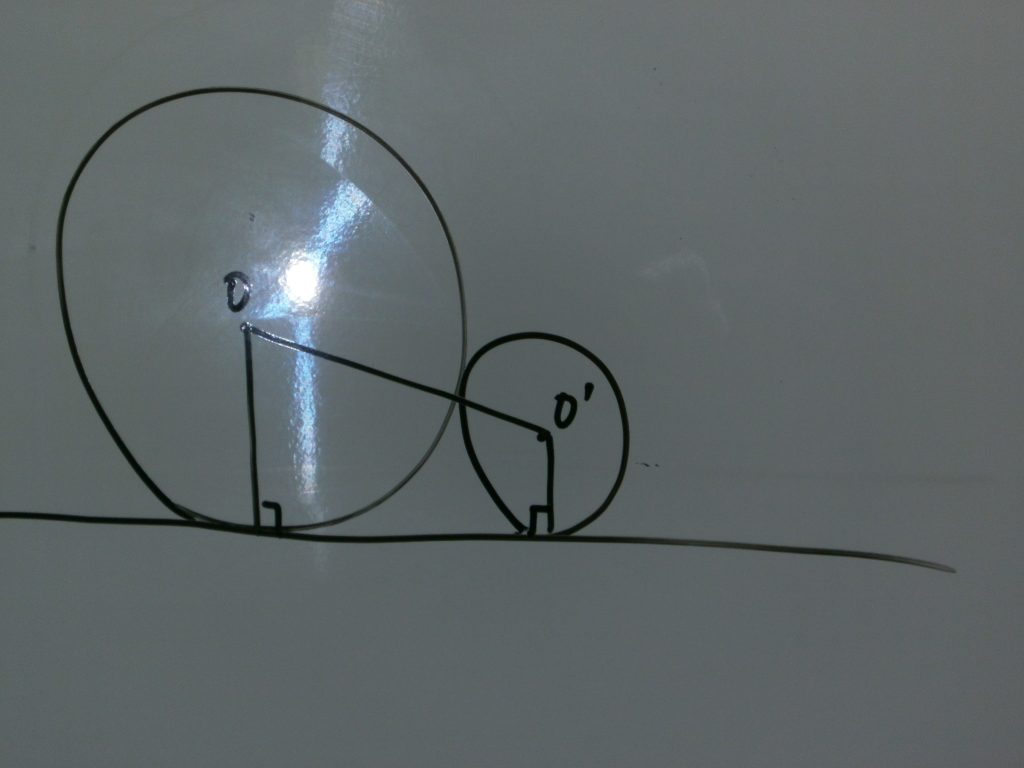
三平方では、円と直線や図形が絡んだ問題があります。
上の問題のようなタイプでは、補助線が必要です。
定期試験によく出る問題ですが、出来ない生徒さんをよく見かけます。
さらに、上のような問題だと補助線の数が増えます。
ここまでくると、お手上げ状態の生徒さんも出てきますね。
でも、安心してください。
ちゃんと、体系数学問題集を解いていれば大丈夫です。
最初は、解けないかもしれません。
解けなかったら、解答をよく見て解き直してください。
そのうち解けるようになります。
相似との融合問題
三平方の定理と相似を絡めた問題もよく見かけます。
”三平方の定理”の単元だからと言ってそれだけで解ける問題ばかりではありません。
線分の長さを求める問題では、相似は大活躍です。
相似が苦手な人も多いですが、試験までに復習しておいた方が良いかもしれませんね。
上のような直角三角形ABCにおいて、AからBCに垂線を引いた場合に相似の三角形がいろいろ出てきます。
まず、三角形ABCと三角形DBCは相似です。
同様にして、右の三角形ACDも大きい三角形と左の三角形も全部相似になっています。
直角三角形の問題であれば、三平方の定理はもちろん使えます。
けれども、それだけだTお解けない問題が多いです。
問題のどこかの部分で相似を使って長さを出すのが必要になります。
間違いやすいのは、どこの辺とどこの辺が対応しているのかです。
意外と分かりにくいことが結構あります。
そういう時には、等しい角に注目してその角の対辺という見方をすると対応する辺を間違えることが少なくなります。
空間図形となると
平面だけでも大変な三平方の定理
なんと、立体の問題も出てきます。
切断面を考えないといけない問題は、得手不得手がはっきりと分かれます。
体積を求める問題だと、工夫しないと膨大な計算量となります。
まあ、いきなり空間の問題は解けないので平面の問題が解けるようになってからの方が良いでしょう。
三平方の定理の空間の問題を与えられた図だけを使って、解こうとする人が多いんですが、そのやり方だと解けないことが多いです。
ちゃんとこうとしたら、切断面の平面図をちゃんと書かなければいけません。
切断面の平面図と各頂点をちゃんと記号で記入します。
そういった平面図を何枚か用意して、もともとの見取り図と照らし合わせながら考えるわけです。
空間の問題はその直感的に解くということができる人はそんなに多くありません。
やはり平面図で自分の目で確認して解くっていう作業がどうしても必要になります。
学校の定期テストのレベルで点数を取ろうとしたら、やはりこういった平面図を自分で書かないと始まらないですね。
三平方の定理の範囲の定期試験で点数を取るには
点数が欲しいならば問題演習をやらないといけません。
特に学校から渡されている教材は必ず解きましょう。
一度やっただけで出来ると思っている生徒さんが多いですが、ダメですね。
解けなかった問題は、解き直しをして確実に解けるようになっているか確認することが必要です。
問題によっては、知っていればすぐに解けることもありますよ。
三平方の定理が終わったらいよいよ高校生の範囲に
体系数学で”三平方の定理”が終わるといよいよ高校生の教材に移行します。
そのまま体系数学３を使う学校もありますが、そうでない学校の方が多いようです。
数学に不安を感じている生徒さんは、これまでの範囲の復習をやっておいた方が良いかもしれませんね。
特に、代数の範囲で出来ないところがあると大変なことになります。
体系数学2の次は、普通の高校用の教科書を使うところが多いです。
問題集は、4STEPが多いです。
（一部、サクシードを使っている所が有ります。）
高校の範囲になると差が一気に広がります。
勉強しない人は、一気に置いて行かれます。
そうならないように普段の勉強を頑張らないといけませんね。
学校で参考書をもらうところとそうでない学校があります。
自分で数学の参考書を買うのであれば、フォーカスゴールド”をお勧めします。
今までの、標準であった青チャートよりもカバーできる範囲が広くなっています。
フォーカスゴールドには、大まかな偏差値対応が載っています。
それを見ながら自分が到達しなければいけないレベルを確認しながら勉強を進めると良いでしょう。
個人指導シグマは、中高一貫校専門
オンラインの授業にも対応しています。
体系数学でお困りの方は、お気軽にお問合せください。
