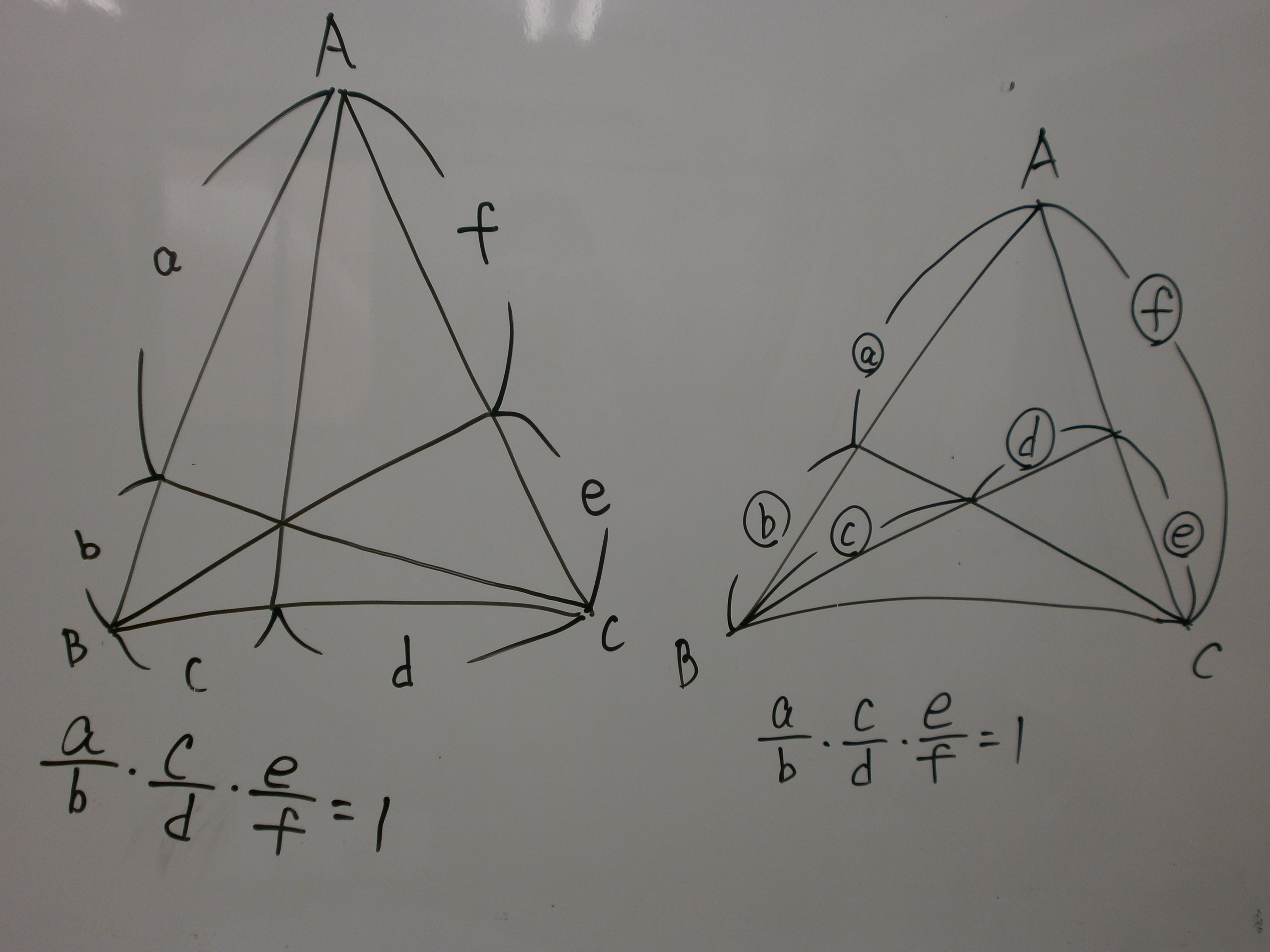
計算はそこそこできるけど、応用問題が苦手な人はいませんか?
個人指導シグマの生徒さんの中には、かなりの割合でいます。
中学受験を経験した生徒さんは、おおむね文章題も出来ます。
しかしながら、付属の小学校から上がってきた生徒さんたちは、残念ながら応用問題ができません。
中学校に外部から入ってきた生徒さんは何の問題もなく解きます。
旅人算や食塩水の問題などは、中学受験の時に解きまくっています。
そんなに応用問題やってない内部進学の生徒さんはどうすれば・・・・
体系数学1で出てくる文章題
体系数学1(代数編)では、正負の数式の計算、文字式、 方程式 、不等式、 関数 を内容を学習します 。
各単元で文章題は出てきます。
.正負の数
正負の数 の単元は 計算が中心です。
なので、 ここで出てくる文章題はほとんどないです。
仮の平均を使った問題 ぐらいでしょうか?
後は、魔法陣とか
仮の平均は、面積図を書けばとても簡単です。
が、面積図をそもそもかけない人が多いのも事実です。
書く努力をしましょう。
文字式
文字式の単元で、文章題と言えば式の証明
”偶数+奇数が奇数になることを証明せよ”
こういうタイプは 証明自体が初めての生徒さんが多いので、苦手な人が多いですよね。
”連続する3つの数の和が3の倍数にないこと証明せよ”
なんて問題も有ります。
この3つの数を文字を使って表すことが出来れば簡単です。
けれも 、なかなかできないですね。
方程式・不等式
方程式になると本格的に 文章題が出ます。
体系数学だと連立方程式も当然のことが出てきます。
そんな中で、 生徒さんが苦手なのは
距離
食塩水
売買損益算
割合
この辺りが苦手な人 非常に多いです。
一つ一つ潰していけば、 そんなに難しくありません。
でも、なかなかちゃんと出来る様にならない人多いですね 。
”3%の食塩水100gと7%の食塩水200gを 混ぜて 5%にする。”
このぐらいの問題は、軽く解けないといけません。
これがわからないと本当に大問題ですです 。
まずは、標準的なレベルが きちんと解ける様にしましょう。
最初に克服すべき ハードルだと思います。
距離の問題に関しても苦手な人が非常に多いんです。
見てると、苦手な人は、そもそも単位の変換が出来ないことが多いです。
時速から分速にできないのです。
距離の問題では、図を描くのが一般的です。
でも、文章題が出来ない人は図が描けないことが良くあります。
いままで、書いたことが無いというのも原因の一つです。
図を描かないと、問題の全体像が掴めません。
そうすると、何をやっていいのかわからないんですね 。
ちょっと大変です 。
文章題は、基本的には求めるべきものを X とか Y とか置けば 良いです。
それで式を作ればいいんです。
距離とか 時間をに注目して等式 を作ります。
特殊な問題に関しては、速さに注目して 方程式を作ることもあります。
それは応用になるとは思います。
まずは、基本問題がちゃんと解けるのが一番
そこから初めて、ちょっとずつ問題の難易度を上げましょう。
不等式の文章問題は、方程式とそんなに変わりません。
不等号の向きに気を付けて解くだけです。
出てくる文章題のタイプも方程式とほとんど同じです。
関数
関数でも、文章問題は出ます。
関数の文章問題は、関数の単元の最後です。
水槽に水を入れる問題
速さの問題
長方形の上を 点が移動してできる三角形の面積
動点処理
このあたりでしょうか?
場合分けが必要な問題も出てきます。
場合分けに慣れていない人が多いので苦戦するところです。
” 1次関数で点が移動して他にも連動して動く点があった時にできる四角形が正方形になるのは?”
このタイプの問題では、x座標を t とおいて y 座標も t を使って表し、それから 方程式を作ります。
なかなか難しいですね。
難しいのはしょうがないんですけども 、 学校でやるのであれば 、こういう問題にも慣れないといけないですね 。
やればできる
はい、やれば出来ます。
やらないと、出来ません。
諦めたら、そこで終わりです。
中学受験で入ってきた生徒さんも文章題をたくさん解いたから出来るようになっただけです。
今、文章題が苦手なあなたもやれば出来る!
附属小学校から上がってきた人は、焦らずに少しずつ解ける問題を増やしてください。
また、外部から入ってきた人も、中学受験のやり方で解けるからと満足してはいけません。
ちゃんと方程式をつくれるようにならないと学習が進むと太刀打ちできなく成ります。
食塩水の解き方
食塩水は、苦手な人が多いですね。
でも、安心してください。
基本的なパターンさえ身に着ければ大体の問題は解けます。
解く際に、図を描くのは当たり前です。
食塩の量の求め方さえ分かれば大丈夫・・・・
もう少し高度な問題になると、2種類の食塩水を混ぜる作業を複数回繰り返します。
このレベルになると、違う考え方を導入した方が簡単に解けるようになります。
解く際のポイントは食塩の量を常に意識して式を立てることです。
速さの解き方
中学受験では、定番の速さの問題
でも、内部生はそんなにやっていません。
やってないから、線分図の書き方もわかってないことも多いです。
速さの問題は、パターンが多いので少し時間がかかります。
焦らずに少しずつ出来る範囲を広げましょう。
速さ・時間・距離の関係は絶対に押さえておきましょう。
基本的には、距離と時間に注目して方程式を作ることが多いです。
時間をxと置いたならば、距離に注目しましょう。
距離をXと置いたら、時間に注目です。
連立方程式になっても考え方は一緒です。
2桁の数の解き方
2桁の数で十の位と百の位を入れ替えた時の大小関係の条件が与えられます。
10x+y=2(10y+x)-4
x+y=14
の様に式化すれば後は計算するだけ。
そんなに難しくありません。
何をやればよいのか
自分に合った問題集が必要です。
学校で配布されたもので間に合うならばそれを使えばよいです。
国立大学付属中学の場合は、配布された問題集が簡単すぎるので違うものが必要です。
個人指導シグマっでは、生徒さんのレベルに合わせていくつか教材を用意しています。
keyワーク
新中学問題集
体系数学代数編
新Aクラス問題集
などなどです。
どうやれば・・
とにかく解くことが大切です。
一定量の学習は絶対に欠かせません。
その上で、個々のパターンをちゃんと理解して解けるようにするべきではないでしょうか?
成績の差が広がる中学1年生の2学期
後で後悔しないで済むように、したいものですね!
全く分からないのならば、教科書の例題の解法を真似しましょう。
ぞを自分で書くと理解が進みます。
息詰まったらシグマに
1年生で困る 文章題について書いてきました 。
出来ない自分が特殊だと考える必要はないです。
しかし 、勉強すれば何とかできる範囲 なので 、自分でちゃんとやるって事は大事です 。
基本的には解決を何回も解く
そしてわからなかったら、解答を見てじっくりと考える 。
ここで考えて自分で理解するって プロセスが絶対必要です。
ただ単に、説明を受けて分かった分かったっていう風になってもあっという間に頭から消えてしまいます 。
自分でしっかり考えて納得いった事は、そう簡単に頭から消えません。
考えるっていう プロセスを経てから解法 を身につけるという風に考えてください 。
その方がうまくいくと思います。
で自分でやってわからなかったら、解説を見る。
それでも分からない物も あると思います。
そしたら 、学校先生に聞くなり友達に聞くなりしてもいいと思います。
でそれがなかなか難しい人もいるかもしれません。
そういう人は 、個人指導 シグマ までお問い合わせください。
中高一貫専門ですので、 体系数学の指導はお任せです。
体系数学 コースもあります。
体系数学コースならば、学校 使ってる 問題集 も 使えます。
さらに動画サポートがついております。
わからない問題もそれを見て何回も何回も見れば 、だんだんわかってきます。
苦手だった 文章題もなんとか 点数が取れるようになってはずです。
個人指導シグマは中高一貫&国立大学付属専門の個人指導
オンライン授業にも対応しています。
お気軽にお問合せください。