体系数学2幾何編は、皆さん大変苦労しています。
と言うのも、相似、円や三平方の定理など重要単元が入っているからです。
それ以外に、三分の一ぐらいは高校生の内容が混ざっていることも苦労する原因です。
この難関の体系数学2幾何編をどうやって乗り切ればいいのか?
第1章図形と相似
相似
相似条件を覚えられない人はほとんどいません。
単純な問題ならば解き方は皆さん分かります。
でも、対応する順に書いてないと減点です。
厳しい学校では、点がもらえません。
中学受験でも相似の考え方を使って問題を解いたはずなので、お馴染みのはずです。
しかし、内容が高度になるのでちゃんと勉強しないと対応できなく成ります。
平行線と線分比
長さを求めるだけなら問題演習だけで何とかなります。
問題は、補助線が必要なものです。
補助線の基本は、
延長
平行線
垂線
角の二等分線
などです。
問題ごとに必要な補助線が引ける様になるには、ある程度の問題数をこなさないといけません。
補助線に気が付かないと解けない問題も多くあります。
角の2等分線と線分比の関係の証明も自力で出来る様にしておきましょう。
中点連結定理
中点連結定理は、単純ですが意外と利用範囲が広いです。
1:2だけでなく平行条件にも目を向けましょう。
そうすると同位角や錯角も使える様になります。
問題例
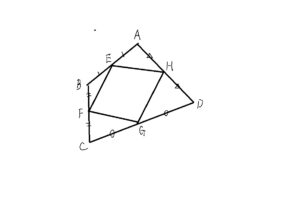
四角形ABCDにおいて各辺の中点をEFGHとする時に、四角形EFGHが平行四辺形であることを証明
これはAC補助線を引いて、三角形BCAで中点連結定理また三角形DACで中点連結定理を用いれば簡単に証明できます。
時々、定期試験に出題されるレベルです。
さらに進んで、四角形EFGHが長方形になるための条件を聞かれることもあります。
面積比・体積比
基本概念は、すぐに理解できます。
でも、応用問題になると意外と正解率が低くなります。
大体は、単純なミスです。
だからこそ、ミスが出ないようになるまで問題を解く必要が有ります。
問題例
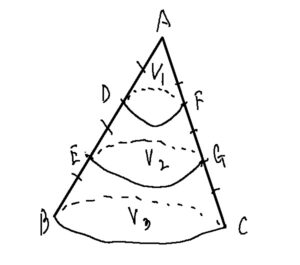
ABを三等分し、底面に平行に切る。その時V1:V2:V3を求めよ。
これちょっと応用問題になります。これ最初に相似な立体を探します。相似な円錐が3種類ありますからそれの相似比が1:2:3なので体積比は1:8:27になります。それから余分な部分を引いて答えを出すような考え方になります。
そうすると
V1:V2:V3=1:7:19が出てきます。
第2章線分の比と計量
線分比と面積比
線分比の所は、内分・外分が分かれば大丈夫です。
基本は、一筆書きです。
最初に覚え間違うと後が大変ですので確認しながら進めましょう。
チェバ・メネラウス
名前で恐れおののく人がたまにいます。
単なる人の名前だから大したこと有りません。
使い方も簡単です。
一度覚えれば、線分比の問題が楽に解ける様になります。
一部の学校の先生が難解な教え方をして生徒さんを混乱させているのを見ました。
理解できないなら、その先生のやり方は無視しましょう。
第3章円
外心・垂心・円周角の定理
円の単元で円周角の定理までは、そんなに難しくありません。
と言っても、中心角と円周角を間違える生徒さんは出てきます。
円周角の問題で間違えていると平均点すら危ういです。
円周角と中心核の関係で円周角の位置が端によると分からなくなる人が多いです。
これは、もとになる弧が何かを意識していないのが原因です。
円に内接する四角形
円周角の定理の延長で理解しやすいところです。
円に内接する4点を見つけてから解く問題になると正解率が下がります。
証明問題もやや難しくなります。
円に内接する四角形の定理の逆も大事です。
同一円周上に4点が載ることが分からないと解けない問題が相当数あります。
最初は、気が付かない生徒さんがほとんどです。
問題数をこなしていくにしたがって、自分で気が付くようになります。
円と接線
接弦定理だけでなく、接線の長さを求めることも必要です。
図形なのに方程式を立てないと解けないことも出てきます。
相似の関係にある三角形も色々と出てきて解くときに迷ってしまいがちです。
接線は、三平方の定理でも出てきます。
接線と接点を通る半径は、直交するので三平方の定理が使えるからです。
方べきの定理
方べきの定理は、相似の応用です。
だから、別に知っていなくても問題は解けます。
でも、知っていた方が早く解けます。
体系問題集のB問題が解けるようにしましょう。
二つの円の位置関係
2円の位置関係を半径と中心間の距離で表せるようにしましょう。
分かりにくければ最初に、内接や外接の場合の等式を覚えましょう。
等式を最初に書いていれば、それ以外の場合は不等号にすればよいのです。
トレミーの定理(発展)
トレミーの定理は、第3章の最後に発展として載っています。
だから、学校で扱わない所も多いです。
でも、証明自体は、読めば分かります。
興味がある方は、一度読んでみてください。
もしもトレミーの定理をベースにした問題が出たら大変有利になります。
オイラー線(コラム)
オイラー線と9点円についてコラムで書かれています。
このレベルで定期試験が出題される学校は、今の所遭遇していません。
でも、長期の休みの研究課題で出している学校は有りました。
確か、フェリス?
第4章三平方の定理
平面
三平方の定理の証明から始まります。
証明方法自体は,たくさんあります。(夏休みの宿題になっている学校も有ります)
授業でやったものは、最低押さえておけばいいと思います。
1:2:√3
1:1:√2
などを使えるのは、当たり前
3編の長さが分かっている図形の面積も出せる様にならないといけません。(補助線が必要)
テストによく出るのは、2円の共通接線の長さを求める問題です。
空間
空間図形は、最短距離を求める問題はそんなに難しくありません。
切断面を自分で考えてそれを複数組み合わせる問題になると難解になります。
円錐の中に2つの球が内接している問題も皆さん間違えることが多いです。
立方体の中に球が3個以上内接するのも大変です。
とにかく、空間図形は難しいところです。
体系問題集のA問題からしっかり学習することをお勧めします。
つまずきやすい単元
相似を複数回使う問題
相似を1回だけ使う問題ならば、そんなに難しくないので皆さん解けます。
でも、何種類かの相似の組み合わせを利用して解いていく問題は苦手にする生徒さんが急増します。
やっていて詰まったら、結論から逆算すると道筋が見えることもあります。
使っていない条件の利用法を考えるのは当然です。
複雑な問題になると図が汚くなります。
分かりやすくするのは、なるべく大きくきちんと書くことです。
面積比・体積比
中学受験を経験した生徒さんは、すでに学習した内容です。
でも、付属の小学校から上がってきた生徒さんや小学校の時の理解が不十分の生徒さんは苦労しています。
基本は相似です。
相似形でないのに、相似比をそのままあてはめて間違えている人も多いです。
でも、問題数をこなせば克服できる単元です。
円の応用問題
オイラー線やフォイベルバッハの定理まで行くと難解です。
トレミーの定理もなかなか手強いですね。
そこまでいかなくとも、円の応用問題はいくらでも難しくできます。
体系問題集に載っている問題は全部出来る様に何回も解くのが近道です。
急に全部解ける様になることは、まれです。
自分のペースで少しずつ前に進みましょう。
円や球の絡んだ三平方の定理の応用問題
円や球が内接する三平方の問題は、難解です。
三平方の定理だけでなく、相似などの今までに習ったことを組み合わせることが多いからです。
授業をやっていても説明すれば理解はしてくれます。
でも、「どうやって、それ思いつくの?」
なかなか自力で解けません。
球の内接問題は、3・4回繰り返してやっと理解できる人の方が多いかもしれません。
立体の切断を要する問題
切断しないと解けない問題も生徒さんが苦手とする分野です。
見取り図のまま解ける人は天才です。
私が解く時は、必ず切断面の平面図を書くようにしています。
それも何枚も書きます。
それらを並べてどこから考えるべきかを判断します。
図形の問題に苦手意識が出たら
1年生の時の三角形の合同の証明は何とか乗り切っても、相似になったとたんに訳が分からなくなる人も多いです。
相似をちゃんと理解しないままに円の単元に入ると自力でなかなか問題が解けなくなります。
単純に角度を出すだけの問題は、練習次第で何とかなります。
でも、証明になるとそうはいきません。
特に幾何2の範囲は、全くわからなくなることが有るので要注意です。
理解が怪しくなったらすぐに個人指導シグマにご相談ください。
同じような症状の生徒さんを沢山見てきましたので、お任せください。
個人指導シグマは、中高一貫専門なので、中学1・2年生は体系数学を指導することが殆どです。
幾何のテストで平均点に行かない生徒さんも沢山見てきました。
全く分からない人は別にして、きちんと解き方を覚えれば皆さん点数は伸ばせます。
もっと得点を伸ばしたい人は、お気軽にお問合せください。
文京区の教室での指導のほかにオンラインの授業にも対応しています。
オンライン授業は、動画でのフォローも付いていますので分からない問題を何回も復習できます。
お問い合わせの方は、下の赤いボタンを押してください。