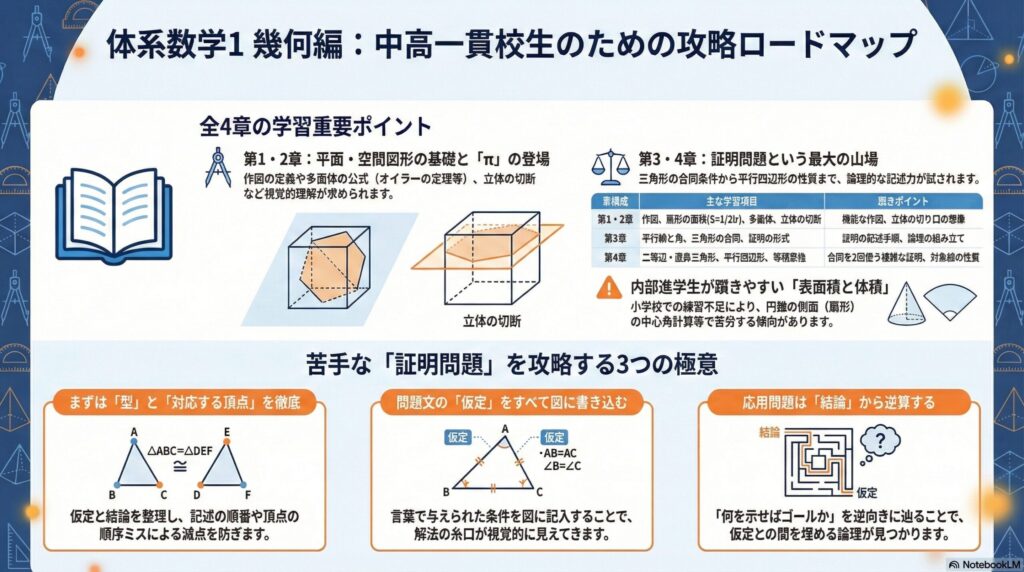
体系数学1幾何編の中で扱われているのは 、公立中学1・2年の図形の内容です。
３章の証明問題のあたりから苦手になる生徒さんが多いです。
体系数学のまとめはこちらから
第１章平面図形
平面図形の基礎
最初に、直線・線分・半直線を学習します。
それから、２直線の位置関係、距離、角、円、円と直線と続きます。
用語の問題として出題される分野です。
図形の移動
小学校でもやった、対称移動、回転移動、平行移動を改めて学習します。
色々な移動を組み合わせる問題も出てきます。
複雑なものは、意外と難しいです。
作図
作図は小学校と違って コンパスと定規だけで書くということをやっていきます。
コンパスの基本的な使い方をちゃんとわかっていない生徒さんがいます。
ちゃんと円が書けないのでずれてしまったりします。
垂直二等分線
垂線
角の二等分線
円の接線
などを実際に作図します。
分かったつもりにならないように、自分で書いて確認することが必要です。
それぞれの線の定義も覚える必要が有ります。
面積と長さ
面積と長さです 。
この辺りは小学校でもやったので皆さん分かっています。
新しく習うことととして、円周率3.14の代わりにπが登場します。
扇形の面積の公式を改めてやりますが、新しい公式も出てきます 。
S=1/2 lrっていう公式です。
この公式を導き出せというような問題も出ることがあります。
この公式を使うと円錐の表面積などを簡単に求めることができます。
第２章空間図形
色々な立体
円錐・角錐や中を最初に学習します。
それから 正多面体に入ります。
正多面体では 各図形の頂点の数 面の数 辺の数を調べたり 、それらの相互関係 （オイラーの多面体定理）を扱う学校も多いです。
さらにこ この分野を詳しく 掘り下げる授業もやっている学校が有ります。
多面体の頂点の数 、例えば サッカーボールにおける 頂点の数などを求めたり する問題出してくるような学校もあります。
空間における平面と直線
2直線の位置関係
直線と平面の位置関係
２平面の位置関係
などを学習します。
空間図形が苦手な生徒さんは、苦戦します。
鉛筆や紙を使って確認しながら進めていく必要が有ります。
立体のいろいろな見方
立体を平面を移動させてできる形にとらえたり、 平面図形を回転してできる形と捉えたりします。
その次に、立体の切断です。
が、立体の切断で切り口を求めるのは結構大変です。
平行な面同士の切り口は平行だっていうことを 突破口にして求めたりします。
延長して1つの平面として考えてやることもできます。
投影図も学習内容に入っています。
立面 図・平面図から 見取り図を作ったりすることはできなければいけません。
展開図は小学校でやった内容です。
正8面体や正12面体になると 苦労する人が多いですね。
立方体の切り口に関しても、色々あります。
３角形、４角形、５角形、６角形
自分で実際に、紙粘土や羊羹を切って確認すると分かりやすくなります。
立体の表面積と体積
立体の体積 ・表面積 は、中学受験を体験した人は問題ありません。
附属小学校から上がってきた生徒さんは、苦手にする人が多いです。
球の体積・表面積の公式を新しく習います。
円錐の側面の中心角も瞬時に出せる様にならないといけません。
円錐の表面積の問題は、附属小学校上がりの生徒さんは例外なく苦労しています。
小学校でそんなに練習していないので、当たり前と言えば当たり前
附属小学校上がりの生徒さんは、おうぎ形の中心角の求め方を知らない人が多いです。
第３章図形の性質と合同
平行線と角
これは 検定教科書の中学校2年生の内容にあたります。
まずは、平行線と角で同位角・錯覚 ・対頂角 など
ちゃんと勉強すれば問題ない範囲です。
角度を出す問題では、補助線が必要になることが有ります。
自分でいろいろ試行錯誤して、個々の問題にあった補助線が引ける様になりましょう。
多角形の内角と外角
外角の定理が出てきます。
小学校でも習っている筈です。
星形の図形の内角の和も入ります。
多面体の内角の和と外角の和もやります。
正多面体の場合は、外角の和の考え方を使った方が早く解ける問題が多いです。
三角形の合同
合同な図形の性質
合同条件
この段階で分からなくなる人はほとんどいません。
証明
ここからが山場です。
仮定と結論を理解してから証明の手順を覚えます。
最初は、何をやっているのか分からない人が出ます。
でも、繰り返してやっていくと 分かります。
見ていると、証明の流れを正しく組み立てることが難しいと感じる生徒が多いです。
基本問題が解けないと、応用問題はお手上げです。
第４章三角形と四角形
二等辺三角形
二等辺三角形の定義や性質
正三角形
逆 と反例
に続きます。
合同の証明の少し複雑なものが出てきます。
直角三角形の合同
直角三角形の合同条件 がここで登場します 。
もちろん 合同の証明 問題も出てきます。
この辺りまでくると、合同の証明問題も複雑になります。
体系 問題集のB問題までは、全部できるように仕上げないといけません。
合同を２回使わないといけない問題も出てきます。
平行四辺形
平行四辺形の性質
平行四辺形になるための条件
色々な四角形
などを学習します。
平行四辺形の5つの合同 条件は図とリンクさせて覚えましょう。
言葉だけで覚えようとしても役にたちません。
長方形・ 菱形・ 正方形などの性質も覚えなければいけません。
それぞれの対角線の性質をちゃんと覚えていない人が多いです。
ベン図を自分で書いて確認するのを勧めます。
平行線と面積
平行線と面積
いわゆる 等積変換になります。
考え方は 中学受験でやってる 生徒さんはもうすでに学習した内容なのでそんなに難しくないです。
一方、内部進学組はなかなか理解できません。
そんなに難しくないのですが、応用問題になると解けなくなります。
単純な等積変換だけでなく、分割して考える問題も出来る様にしましょう。
三角形の辺と角
三角形の辺と角の関係です。
これは高校生の内容がちょっと入っております 。
証明も出来る様にしておきましょう。
体系数学1幾何編では、証明問題に入って苦戦する生徒さんが増えます。
だんだん 、授業についていけなくなる人が出てくるところです。
体系数学1幾何編でちゃんと学習しておかないと、体系数学2の 幾何編で苦労します。
相似が入ってきて問題が難しくなり、分からなくなる人続出です。
みんな苦手な証明問題の解き方
証明の形式に慣れる
証明問題克服の第一段階は、その形式に慣れることです。
証明問題は、記述量が多いので生徒さんは嫌がります。
だから、途中でいい加減な書き方をしてしまうこともあります。
仮定・結論などをまず理解しましょう。
それから、最初は三角形の合同の証明から始める学校が多いでしょうから合同条件を使っての証明をきちんと出来るようにします。
ここで、対応する頂点に気を付けないと減点になる人が出てきます。（採点基準が厳しい学校は、ばつが付きます。）
基本の形が出来てから、徐々に応用問題に進むのがお勧めです。
仮定を全部使う
問題文で与えられた条件は、全部使わないと解けないように問題は出来ています。（一部、例外はあります。）
ここで問題になるのは、数式ではなく日本語で与えられた条件です。
注意して問題文を読まないと、条件を読み落としてしまいます。
そうすると、問題が解けなくなります。
与えられた条件は、図に記入していきます。
そうすると、見通しが良くなります。
図を描かないで解くのは、お勧めできません。
難しい問題は、結論から逆算して方向性を見つける
ある程度、基本問題が解けるようになったら、応用問題ですね。
色々なパターンが出てきます。
でも、どの問題も結論から逆算して考えると解きやすくなります。
ある程度の難易度になると、どこから解けばいいのかわからないことも出てきます。
合同の証明を何種類も組み合わせる必要があることも・・・
そんな時には、結論から逆算してみましょう。
合同・二等辺三角形・平行などなど
逆にたどってみると、仮定との間を埋めていけば理論的には解けることになります。
何をしていいのかわからない状況から一歩先に進むことが可能になります。
個人指導シグマは中高一貫専門だから体系数学にどこよりも詳しい。
オンライン授業にも対応しています。（動画サポートが付きます）
お気軽にお問合せください。
